A Graphical Approach to Remembering the Derivative Formula for Inverse Functions
#post/legacy #calculus #mathematics #writing/guide
This post originally appeared on the very first blog
I have been doing calculus for quite some time now, but there is just one formula that my brain seems to reject—the inverse function derivative formula, which looks like this:
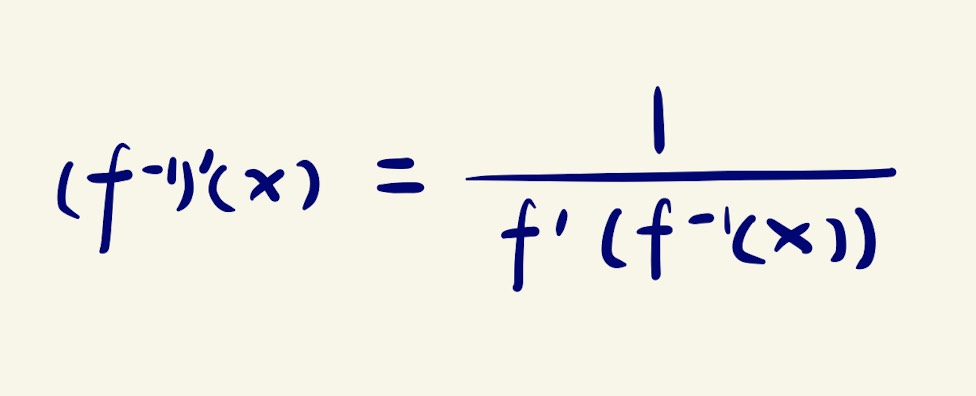
The inverse function rule states that the derivative of the inverse function of $f$ is equal to the reciprocal of the derivative of $f$ of the inverse function of $f$
If you are like me, who hates memorising formulas, you are probably troubled by this obscure equation where inverses and derivatives are all over the place; what’s worse is the combination of inverse and derivative. To make this “easier”, some textbooks decided to use another function $g(x)$ to represent the inverse of $f(x)$. However, does this make it better? Hmmm, not really, at least not to me.
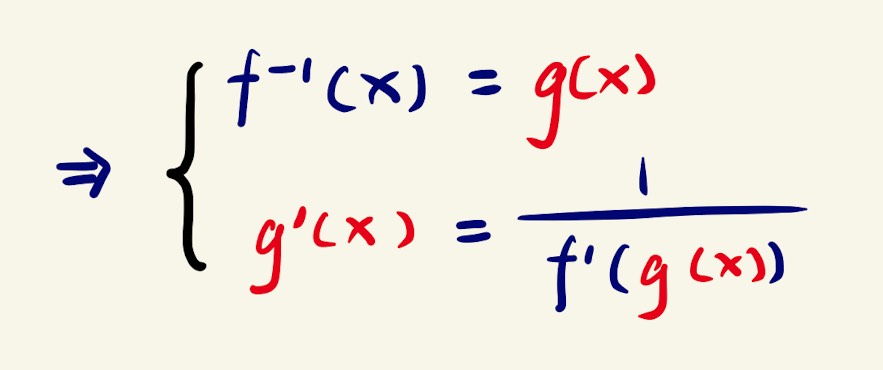
In fact, I forgot this very equation during the AP Calculus AB test last year. Fortunately, I was able to derive it on the fly. So, my goal of writing this article is to convince you that you don’t need to memorise this equation.
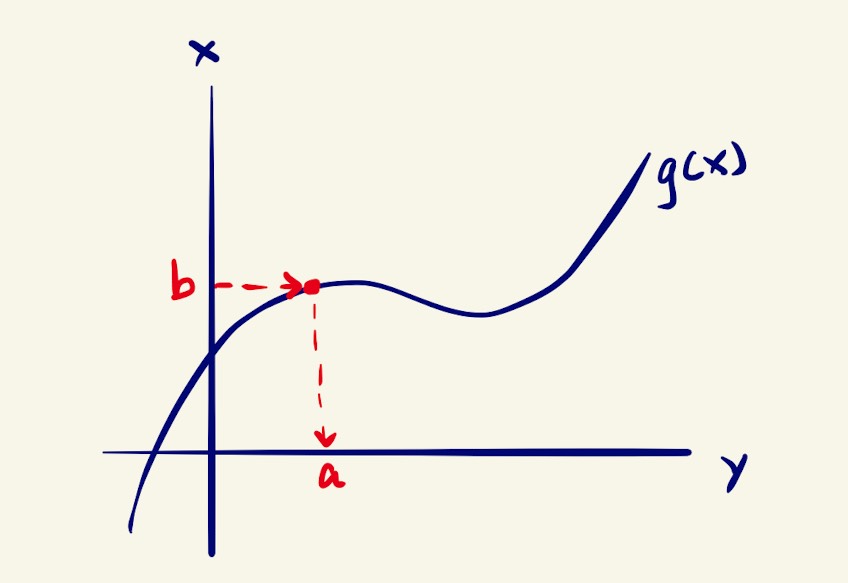
To begin with, let’s first get an intuitive understanding of inverse functions in our head. Consider a function $f(x)$ and let’s feed the function with an input $a$, the function gives an output of $f(a)$, but let’s call this value $b$. Using a graphical approach, the process can be broken down into the following: take the input $a$ and draw a vertical line across it until the line intersects with the curve, then draw a horizontal line from the intersection until it intersects with the y-axis. The y-intersection gives us the value of $b$.
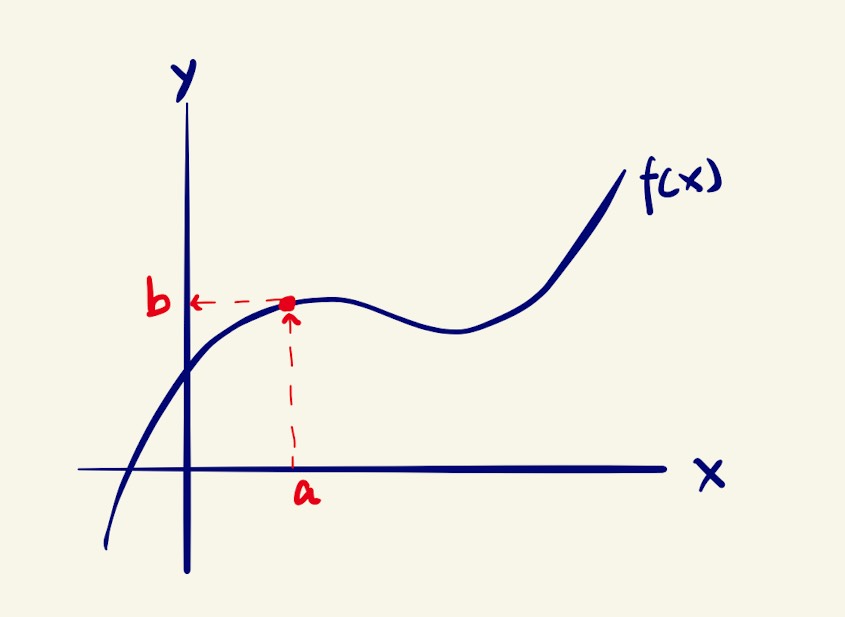
Graphical way to relate the input and output of a function
That probably sounds like something familiar, but let’s see what happens if we use the same idea for the inverse function of $f(x)$.
By definition, the inverse function of $f(x)$, or $g(x)$, should give the output of a when the input is b. In other words, $g(x)$ undoes what $f(x)$ does. On the graph, it looks exactly the same but the red arrows now point in the opposite direction. Noticed that the x and y-axis are flipped because we are using $b$ as input.
If we flip the graph of $g(x)$ to its normal position with the x-axis being horizontal, we can see that $g(x)$ is essentially a reflection of $f(x)$ over the line $y = x$.
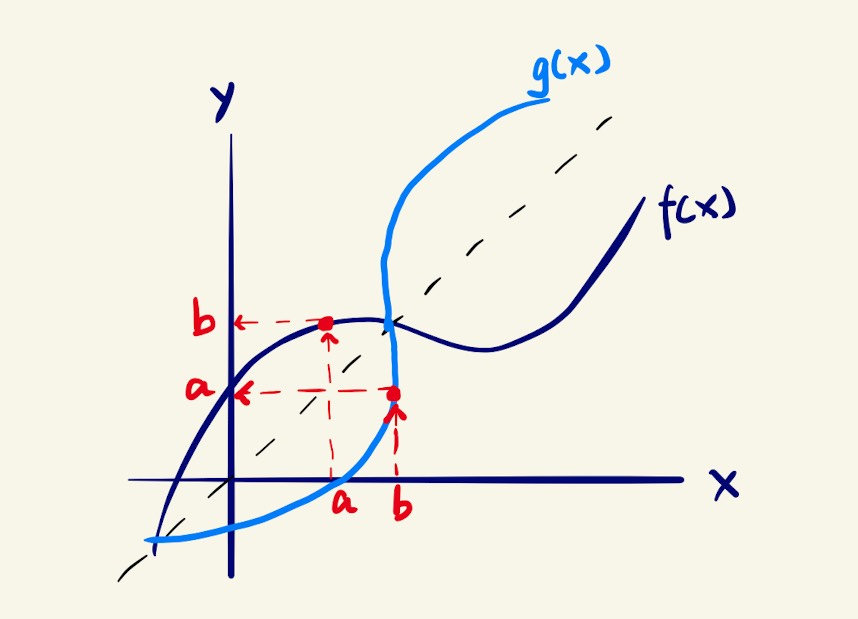
A graph combining $f(x)$ and $g(x)$
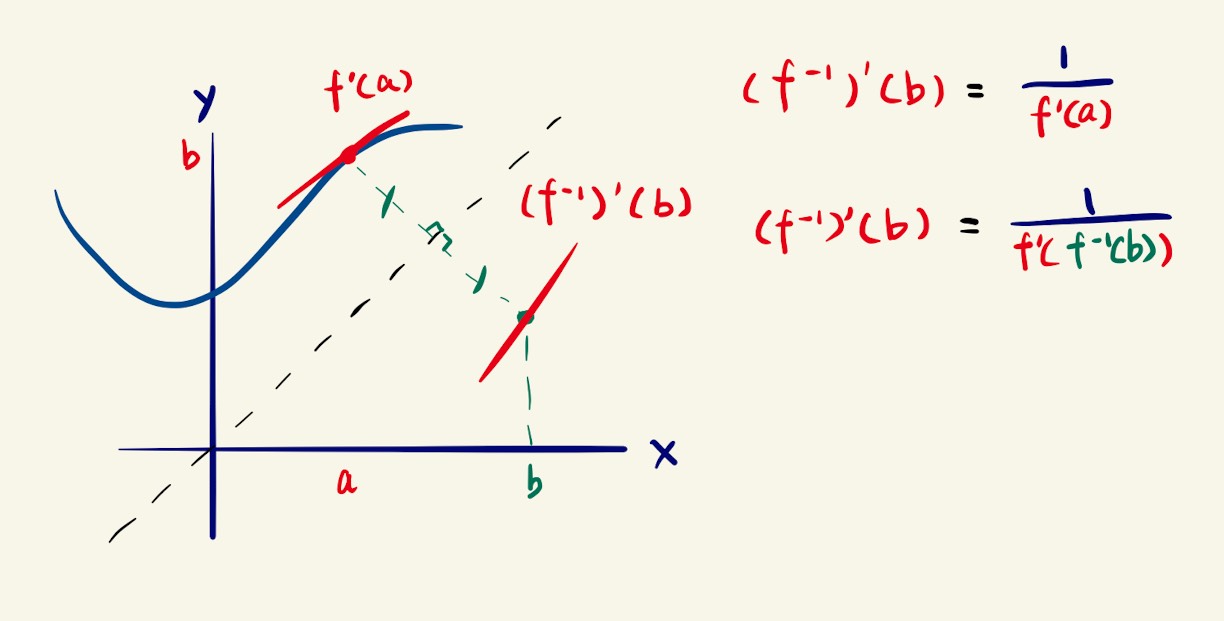
Now comes the fun part. Let’s see what we can do with this graph. If we want to calculate the value of $g(f(a))$, we can first find $f(a)$ by tracing the red rectangle to get $b$. Next, we are going to use the result $b$ as the input for $g(a)$, so we need to get our input $b$ back onto the input axis, or the x-axis. To do this, we simply follow the pink diagonal line as shown in the diagram. Finally, we trace another green rectangle whose vertex is on the curve of $g(x)$. At the end, we get back to $a$, that’s why $g(f(a)) = a$.
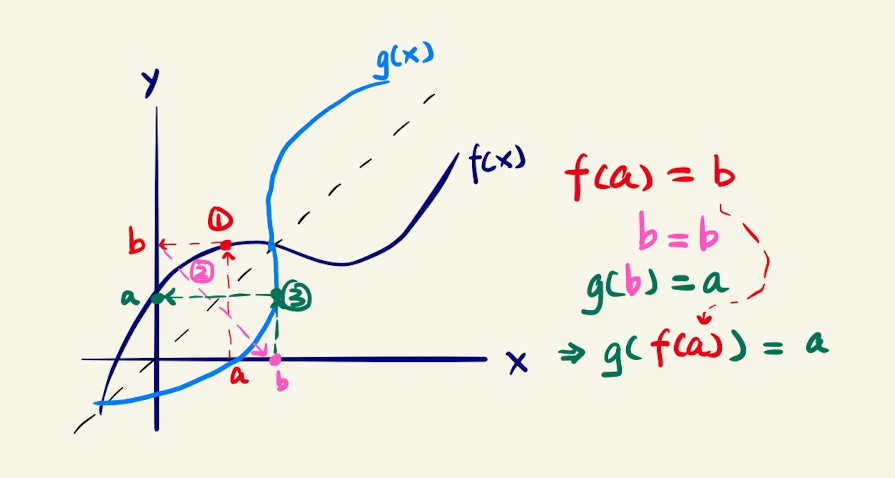
Graphical approach of calculating $g(f(a))$
Okay, that’s good so far, but what does that have to do with derivatives? Don’t worry, we have just our way cleared for that, now let’s dive in. By tracing out rectangles to go back and forth between $a$ and $b$, we get two vertexes whose coordinates are $(a, b)$ and $(b, a)$. By drawing two tangent lines to the graphs at these two points, we get two lines with slope $g’(a)$ and $f’(b)$ respectively, as shown in the diagram below.
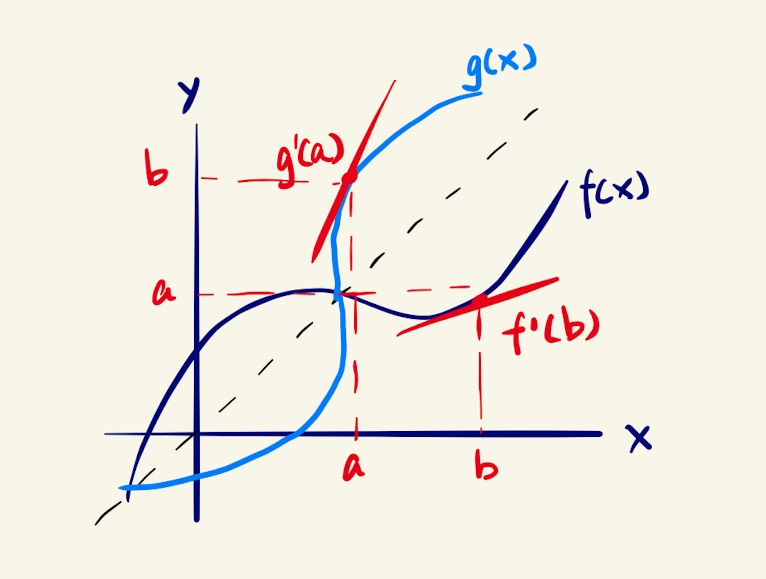
Tangent lines at $g(a)$ and $f(b)$
Notice that since the two curves are reflections of each other about $y = x$, their tangent line must also be reflections of each other about the $y = x$, meaning that the angles they make with $x = y$ are equal in magnitude. If we examine the angles, we can come to the conclusion that the two triangles in the diagram below are also reflections of each other, implying that they are congruent. Using this fact, we can deduce that these two triangles have equal side length.
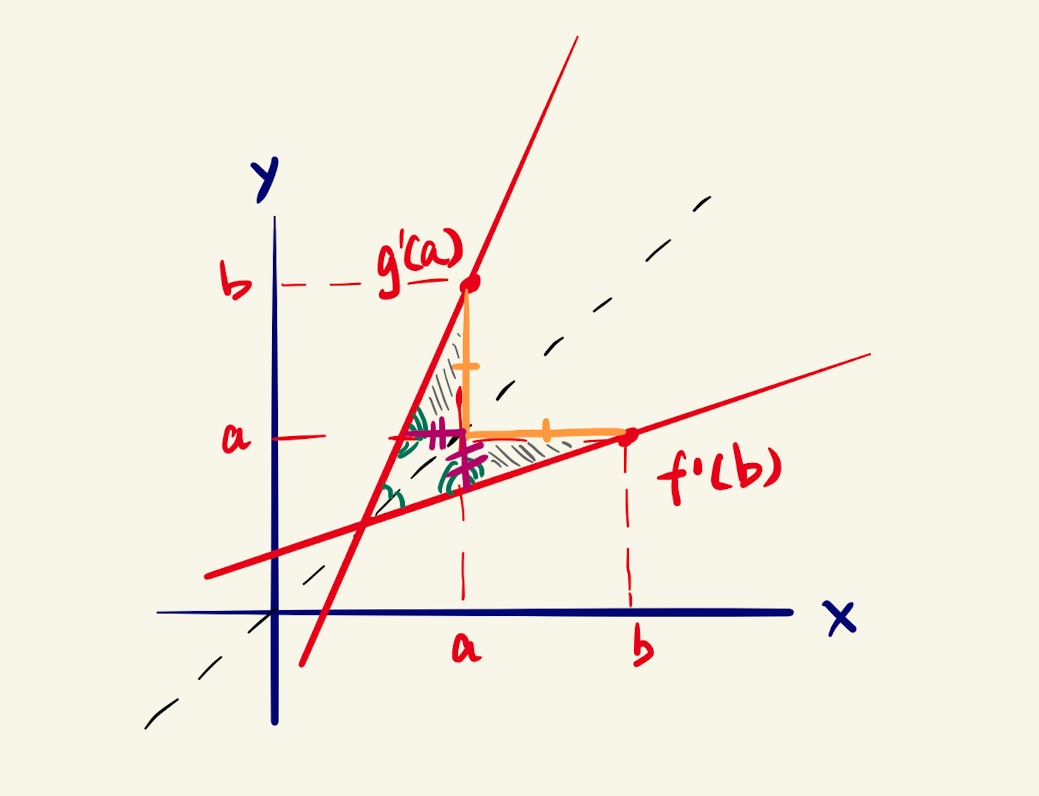
The two shaded triangles are congruent and therefore have equal side length as marked
Now comes the algebra. By denoting the side length of the two triangles with Δx and Δy, we can show that the slope of the two lines are reciprocals of each other, which simply means that flipping the denominator and the numerator of the fraction can get you from one to the other (shown in the diagram). Then, by replacing the Leibniz’s notation with Lagrange’s notation, we can see that the reciprocal of $g’(a)$ is equal to $f’(b)$; note that $Δx$ and $Δy$ are equal to $dx$ and $dy$ for any straight lines. Furthermore, recall the fact that $b = g(a) = f-1(a)$, we can substitute $b$ with $g(a)$ and $g(a)$ with $f-1(a)$. BINGO! We have just derived the formula for differentiating inverse functions.
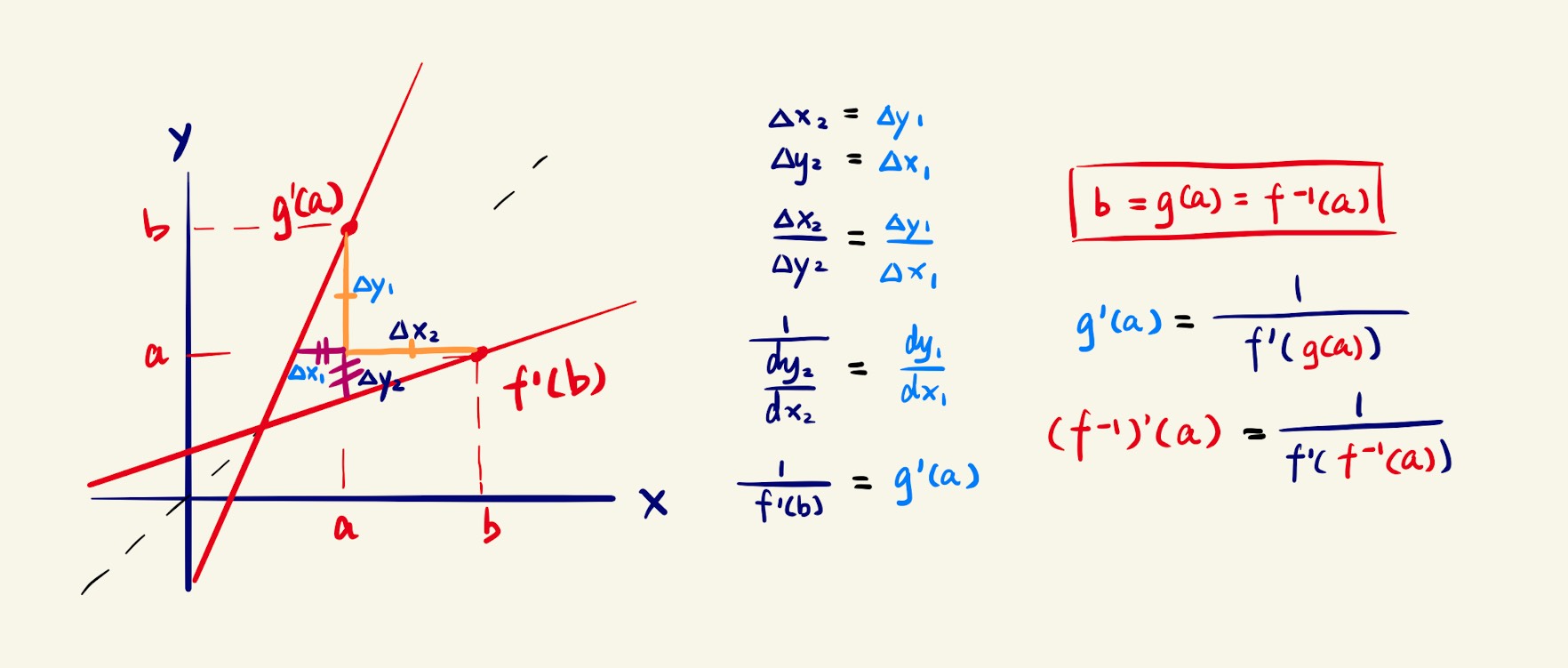
Final touches of algebra
H3 Conclusion
At this point, perhaps you are just thinking: “So what? I suppose in the end remembering the formula is easier than remembering the derivation?!” Well, here is how you can apply the geometric approach to questions without using the formula.
Suppose that you are given the following question:
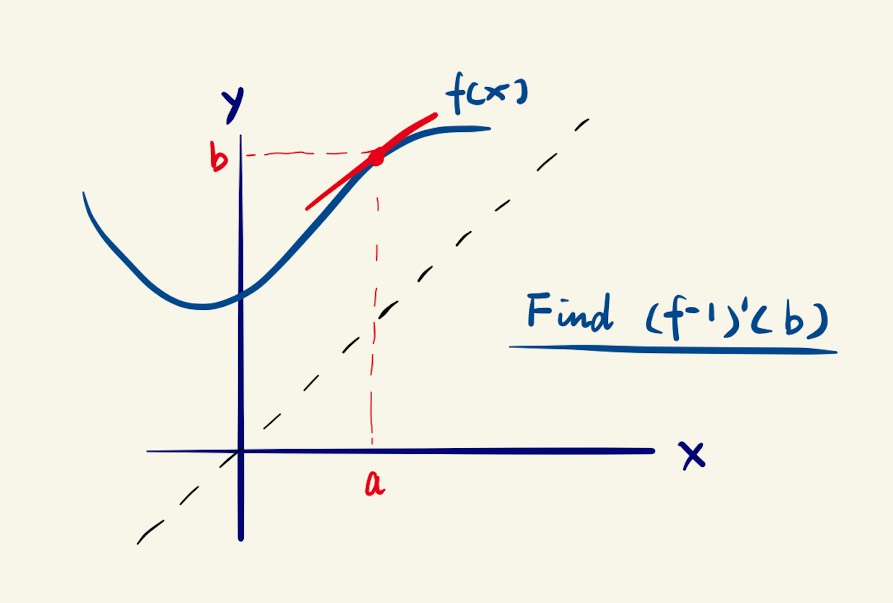
To apply the graphical approach, you just have to remember that the slope of the inverse function a point on the other side of the axis of reflection is the reciprocal of its original slope before the reflection. So all you need to do is draw the reflected tangent line and its slope would be $\frac{1}{(f’(a))}$. Replacing the value of $a$ using the rectangle tracing method, you can get the slope of the inverse function for you particular question! :D
